Insights into Ordinal Embedding Algorithms: A Systematic Evaluation
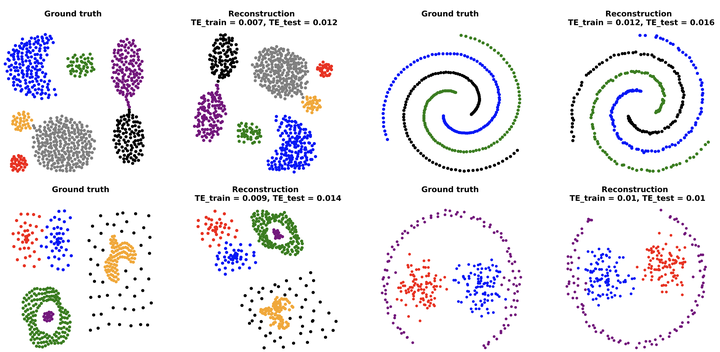 Reconstructing 2D datasets using triplets
Reconstructing 2D datasets using tripletsAbstract
The objective of ordinal embedding is to find a Euclidean representation of a set of abstract items, using only answers to triplet comparisons of the form ``Is item $i$ closer to the item $j$ or item $k$?''. In recent years, numerous algorithms have been proposed to solve this problem. However, there does not exist a fair and thorough assessment of these embedding methods and therefore several key questions remain unanswered - Which algorithms scale better with increasing sample size or dimension? Which ones perform better when the embedding dimension is small or few triplet comparisons are available? In our paper, we address these questions and provide the first comprehensive and systematic empirical evaluation of existing algorithms as well as a new neural network approach. In the large triplet regime, we find that simple, relatively unknown, non-convex methods consistently outperform all other algorithms, including elaborate approaches based on neural networks or landmark approaches. This finding can be explained by our insight that many of the non-convex optimization approaches do not suffer from local optima. In the low triplet regime, our neural network approach is either competitive or significantly outperforms all the other methods. Our comprehensive assessment is enabled by our unified library of popular embedding algorithms that leverages GPU resources and allows for fast and accurate embeddings of millions of data points.